Interpreting machine learning models

Lecture 23

Dr. Benjamin Soltoff

Cornell University
INFO 3312/5312 - Spring 2024

April 23, 2024

Announcements

Announcements

  • Homework 06
  • Friday lab: peer review of draft projects

Goals

  • Review the importance of interpretability for machine learning models
  • Estimate permutation-based feature importance measures
  • Evaluate marginal effects of features using partial dependence plots
  • Generate global surrogates to interpret black-box models

Review: Interpretability

Interpretation

  • How does this model work?
  • Interpretation \(\leadsto\) global methods
  • White-box models lend themselves naturally to interpretation
  • Black-box models require additional effort
  • Prefer model-agnostic methods

Packages for model interpretation

Packages for model interpretation

As of 2020,1 over 30 packages with functions for model interpretation are available in R. Some of the most popular ones include:

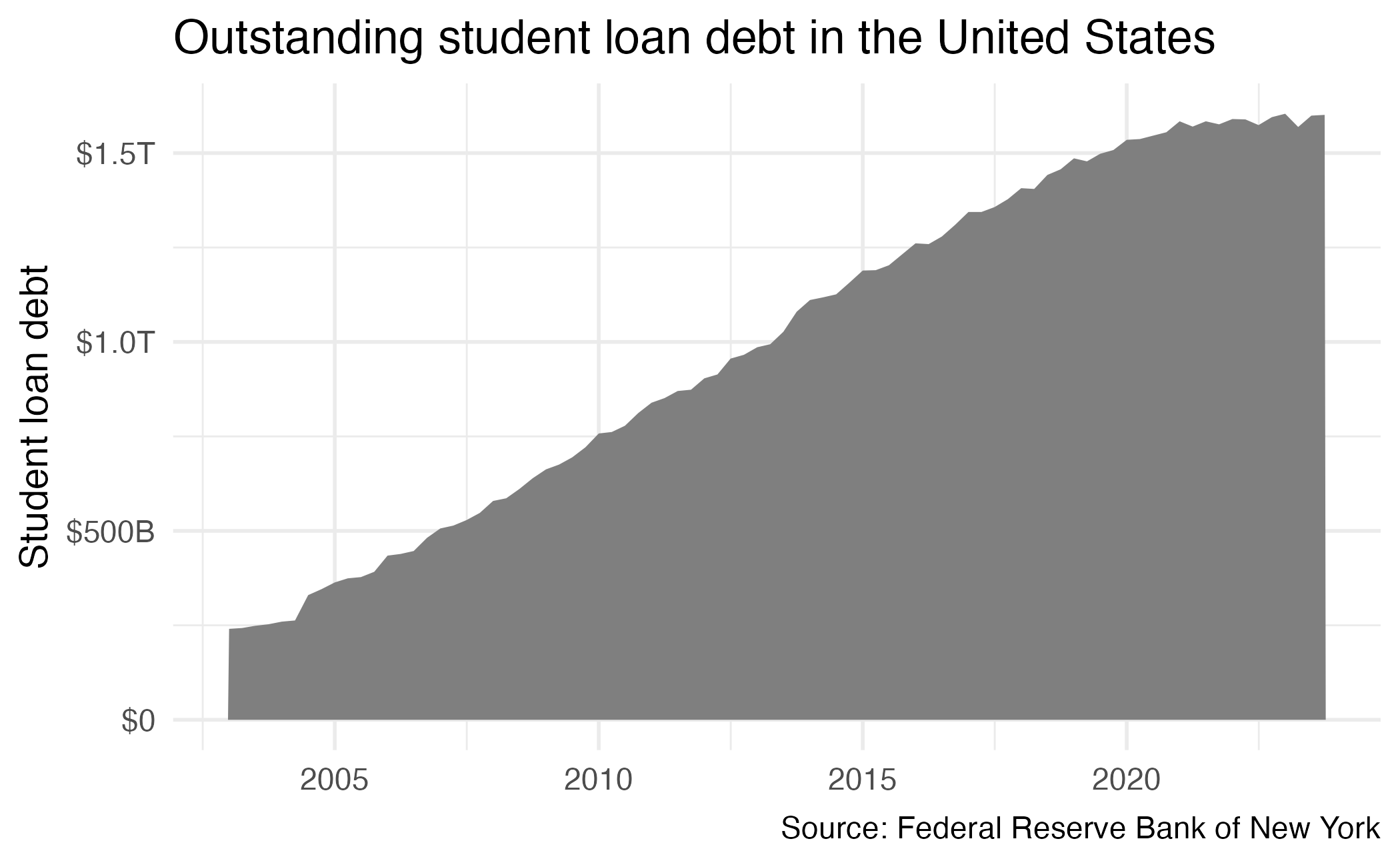
Predicting student debt

ae-20

  • Go to the course GitHub org and find your ae-20 (repo name will be suffixed with your GitHub name).
  • Clone the repo in RStudio Workbench, open the Quarto document in the repo, and follow along and complete the exercises.

Predicting student debt

Predicting student debt

Rows: 1,719
Columns: 14
$ unitid    <dbl> 100654, 100663, 100706, 100724, 100751, 100830, 100858, 1009…
$ name      <chr> "Alabama A & M University", "University of Alabama at Birmin…
$ state     <chr> "AL", "AL", "AL", "AL", "AL", "AL", "AL", "AL", "AL", "AL", …
$ type      <fct> "Public", "Public", "Public", "Public", "Public", "Public", …
$ admrate   <dbl> 0.7160, 0.8854, 0.7367, 0.9799, 0.7890, 0.9680, 0.7118, 0.65…
$ satavg    <dbl> 954, 1266, 1300, 955, 1244, 1069, NA, 1214, 1042, NA, 1111, …
$ cost      <dbl> 21924, 26248, 24869, 21938, 31050, 20621, 32678, 33920, 3645…
$ netcost   <dbl> 13057, 16585, 17250, 13593, 21534, 13689, 23258, 21098, 2037…
$ avgfacsal <dbl> 79011, 104310, 88380, 69309, 94581, 70965, 99837, 68724, 564…
$ pctpell   <dbl> 0.6853, 0.3253, 0.2377, 0.7205, 0.1712, 0.4821, 0.1301, 0.21…
$ comprate  <dbl> 0.2807, 0.6245, 0.6072, 0.2843, 0.7223, 0.3569, 0.8088, 0.69…
$ firstgen  <dbl> 0.3658281, 0.3412237, 0.3101322, 0.3434343, 0.2257127, 0.381…
$ debt      <dbl> 16600, 15832, 13905, 17500, 17986, 13119, 17750, 16000, 1500…
$ locale    <fct> City, City, City, City, City, City, City, City, City, Suburb…

Fitted models

library(tidyverse)
library(tidymodels)
library(rcis)
library(here)

# get scorecard dataset
data("scorecard")
scorecard <- scorecard |>
  # remove ID columns - causing issues when interpreting/explaining
  select(-unitid, -name) |>
  # convert factor to character columns
  mutate(across(.cols = where(is.factor), .f = as.character))

# split into training and testing
set.seed(123)

scorecard_split <- initial_split(data = scorecard, prop = .75, strata = debt)
scorecard_train <- training(scorecard_split)
scorecard_test <- testing(scorecard_split)

scorecard_folds <- vfold_cv(data = scorecard_train, v = 10)

# basic feature engineering recipe
scorecard_rec <- recipe(debt ~ ., data = scorecard_train) |>
  # catch all category for missing state values
  step_novel(state) |>
  # use median imputation for numeric predictors
  step_impute_median(all_numeric_predictors()) |>
  # use modal imputation for nominal predictors
  step_impute_mode(all_nominal_predictors()) |>
  # remove rows with missing values for
  # outcomes - glmnet won't work if any of this column is NA
  step_naomit(all_outcomes())

# generate random forest model
rf_mod <- rand_forest() |>
  set_engine("ranger") |>
  set_mode("regression")

# combine recipe with model
rf_wf <- workflow() |>
  add_recipe(scorecard_rec) |>
  add_model(rf_mod)

# fit using training set
set.seed(123)
rf_wf <- fit(
  rf_wf,
  data = scorecard_train
)

# fit penalized regression model
## recipe
glmnet_recipe <- scorecard_rec |>
  # use median imputation for numeric predictors
  step_impute_median(all_numeric_predictors()) |>
  step_dummy(all_nominal_predictors()) |>
  step_zv(all_predictors()) |>
  step_normalize(all_numeric_predictors())

## model specification
glmnet_spec <- linear_reg(penalty = tune(), mixture = tune()) |>
  set_mode("regression") |>
  set_engine("glmnet")

## workflow
glmnet_workflow <- workflow() |>
  add_recipe(glmnet_recipe) |>
  add_model(glmnet_spec)

## tuning grid
glmnet_grid <- expand_grid(
  penalty = 10^seq(-6, -1, length.out = 20),
  mixture = c(0.05, 0.2, 0.4, 0.6, 0.8, 1)
)

## hyperparameter tuning
glmnet_tune <- tune_grid(
  glmnet_workflow,
  resamples = scorecard_folds,
  grid = glmnet_grid
)

# select best model
glmnet_best <- select_best(glmnet_tune, metric = "rmse")
glmnet_wf <- finalize_workflow(glmnet_workflow, glmnet_best) |>
  last_fit(scorecard_split) |>
  extract_workflow()

# nearest neighbors model
## use glmnet recipe
kknn_spec <- nearest_neighbor(neighbors = 10) |>
  set_mode("regression") |>
  set_engine("kknn")

kknn_workflow <-
  workflow() |>
  add_recipe(glmnet_recipe) |>
  add_model(kknn_spec)

## fit using training set
set.seed(123)
kknn_wf <- fit(
  kknn_workflow,
  data = scorecard_train
)

# save all required objects to a .Rdata file
save(scorecard_train, scorecard_test, rf_wf, glmnet_wf, kknn_wf,
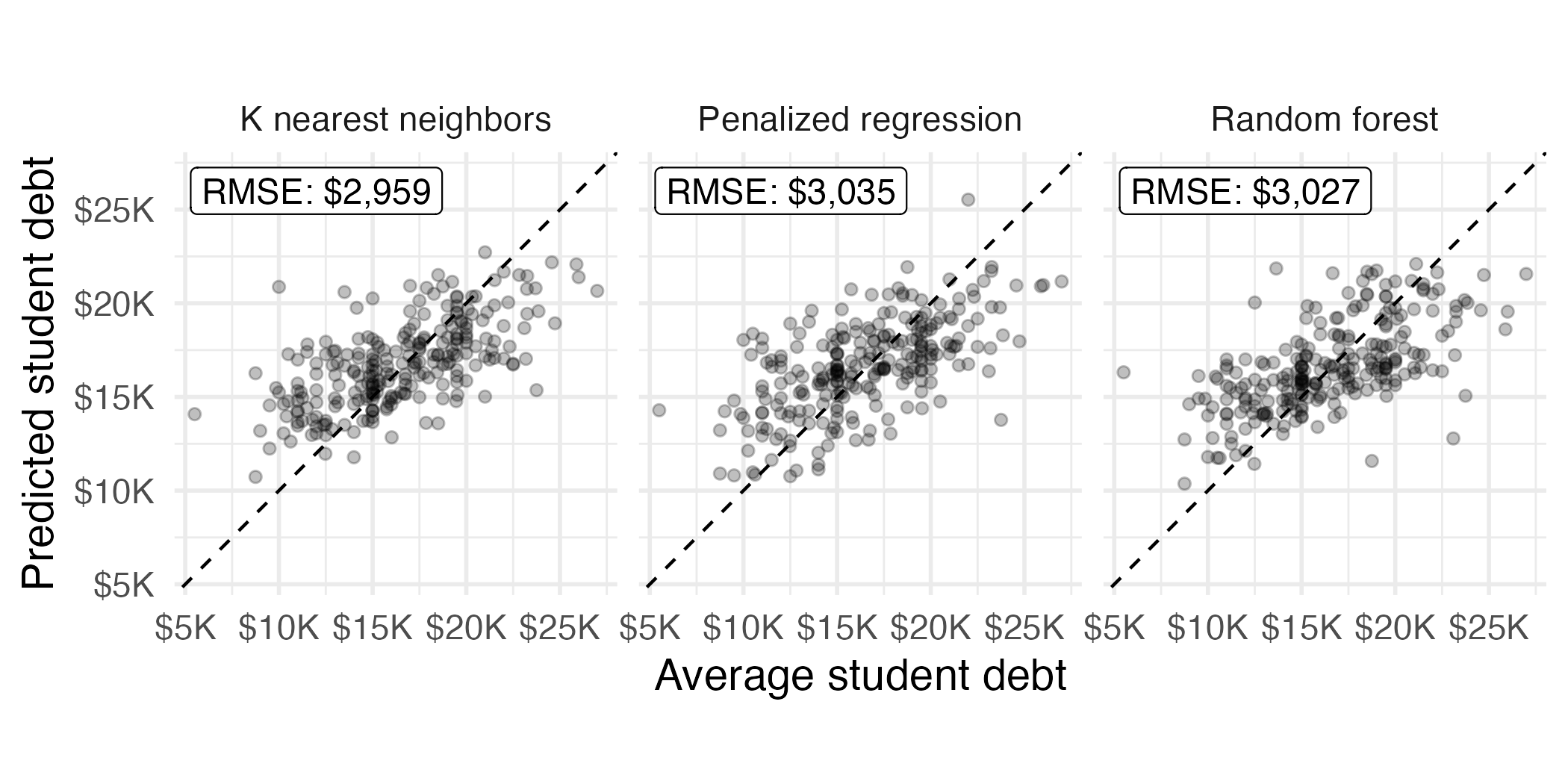
     file = here("ae/data/scorecard-models.RData"))

Evaluating test set performance

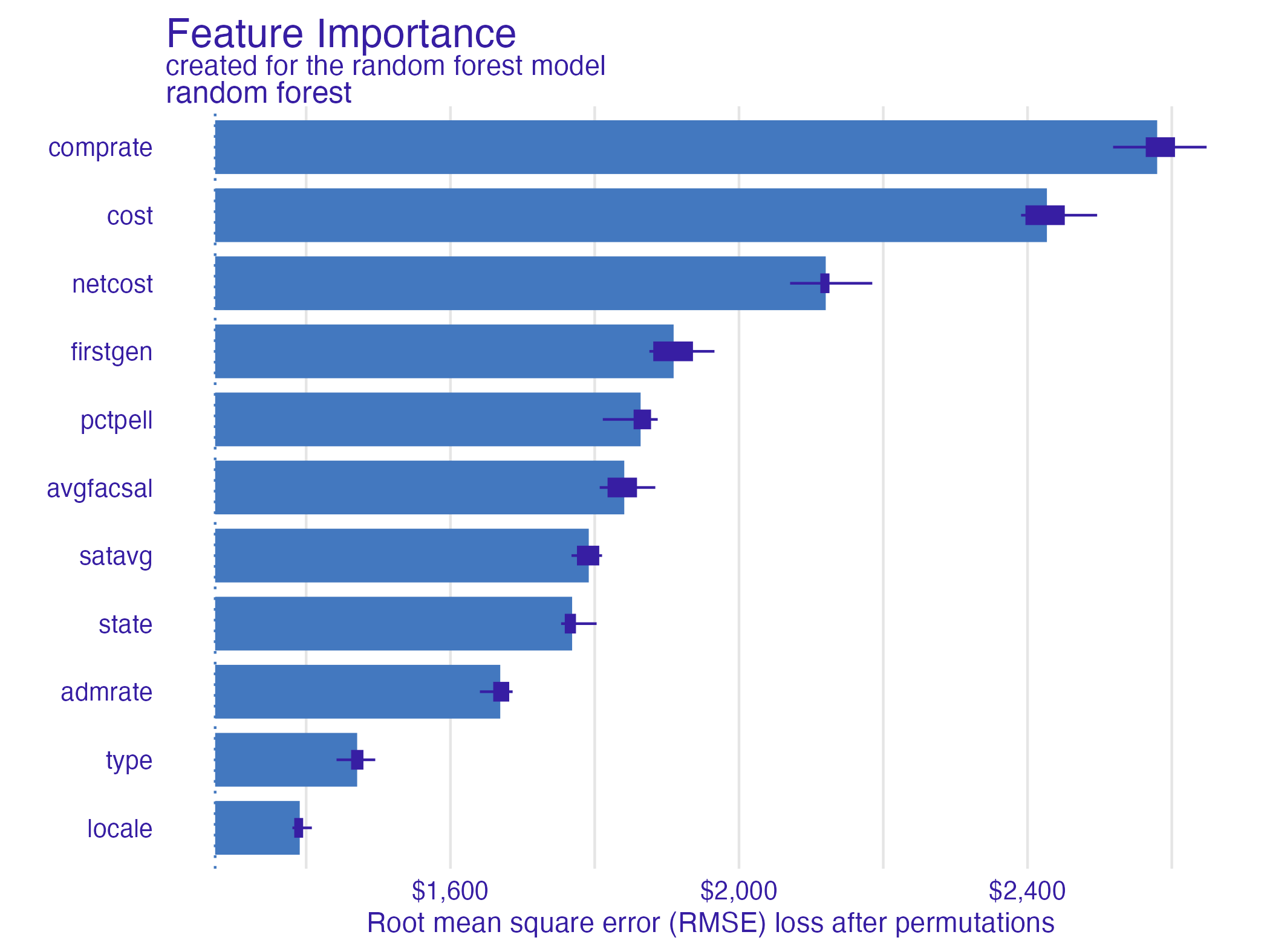
Permutation-based feature importance

Permutation-based feature importance

  • Calculate the increase in the model’s prediction error after permuting the feature
    • Randomly shuffle the feature’s values across observations
  • Important feature
  • Unimportant feature
For any given loss function do
1: compute loss function for original model
2: for variable i in {1,...,p} do
     | randomize values
     | apply given ML model
     | estimate loss function
     | compute feature importance (permuted loss / original loss)
   end
3. Sort variables by descending feature importance

Random forest feature importance

Number of observations permuted

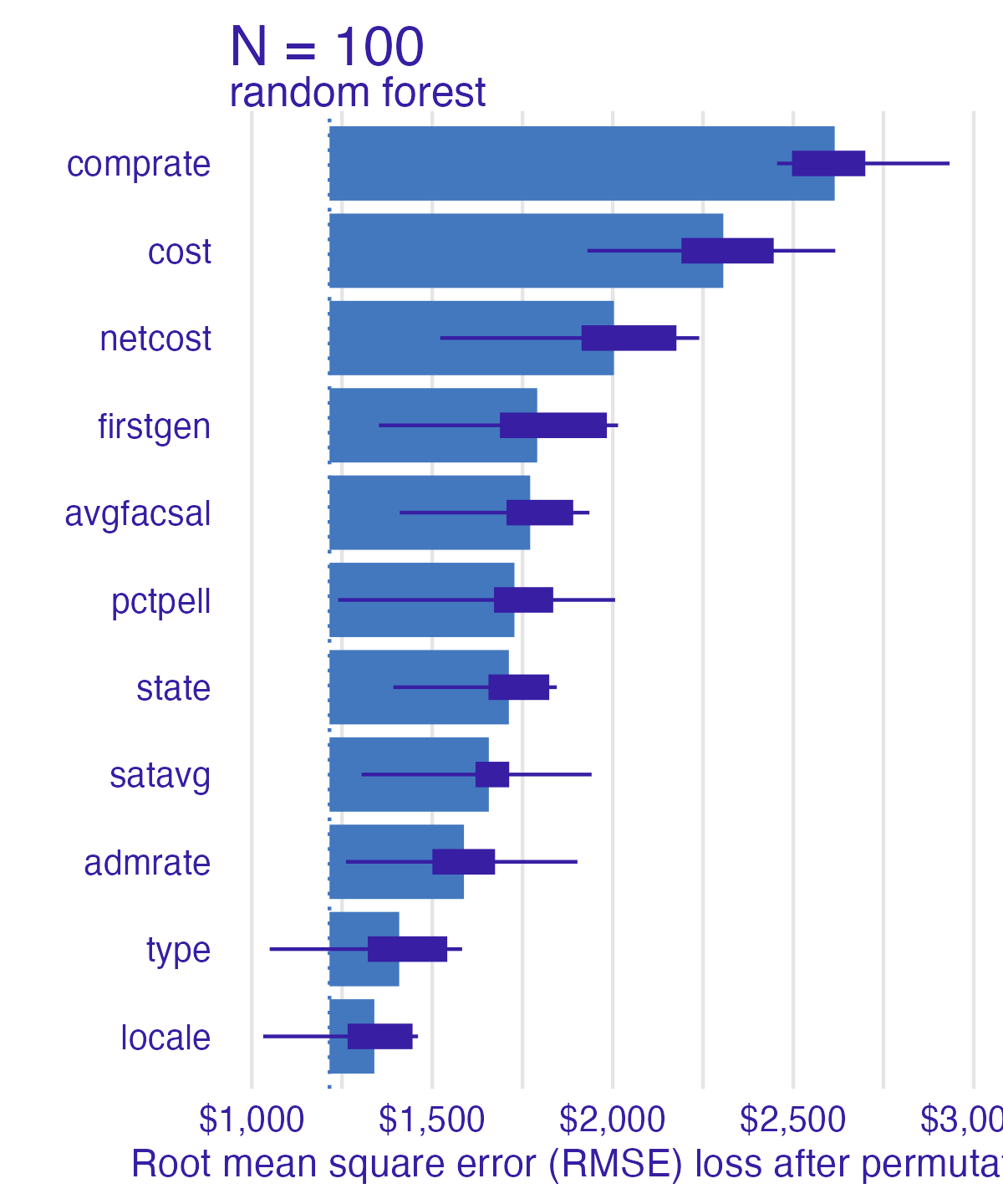
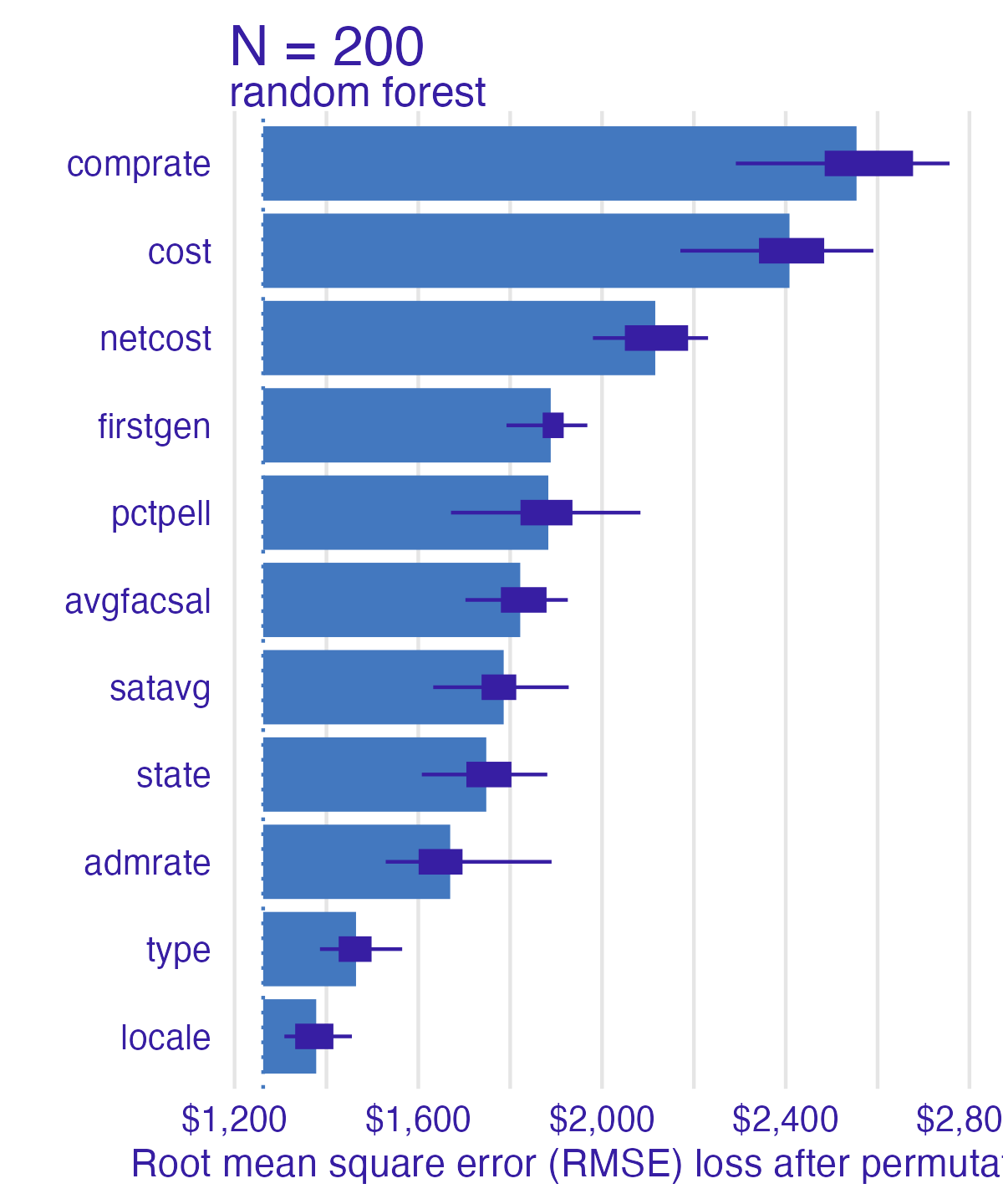
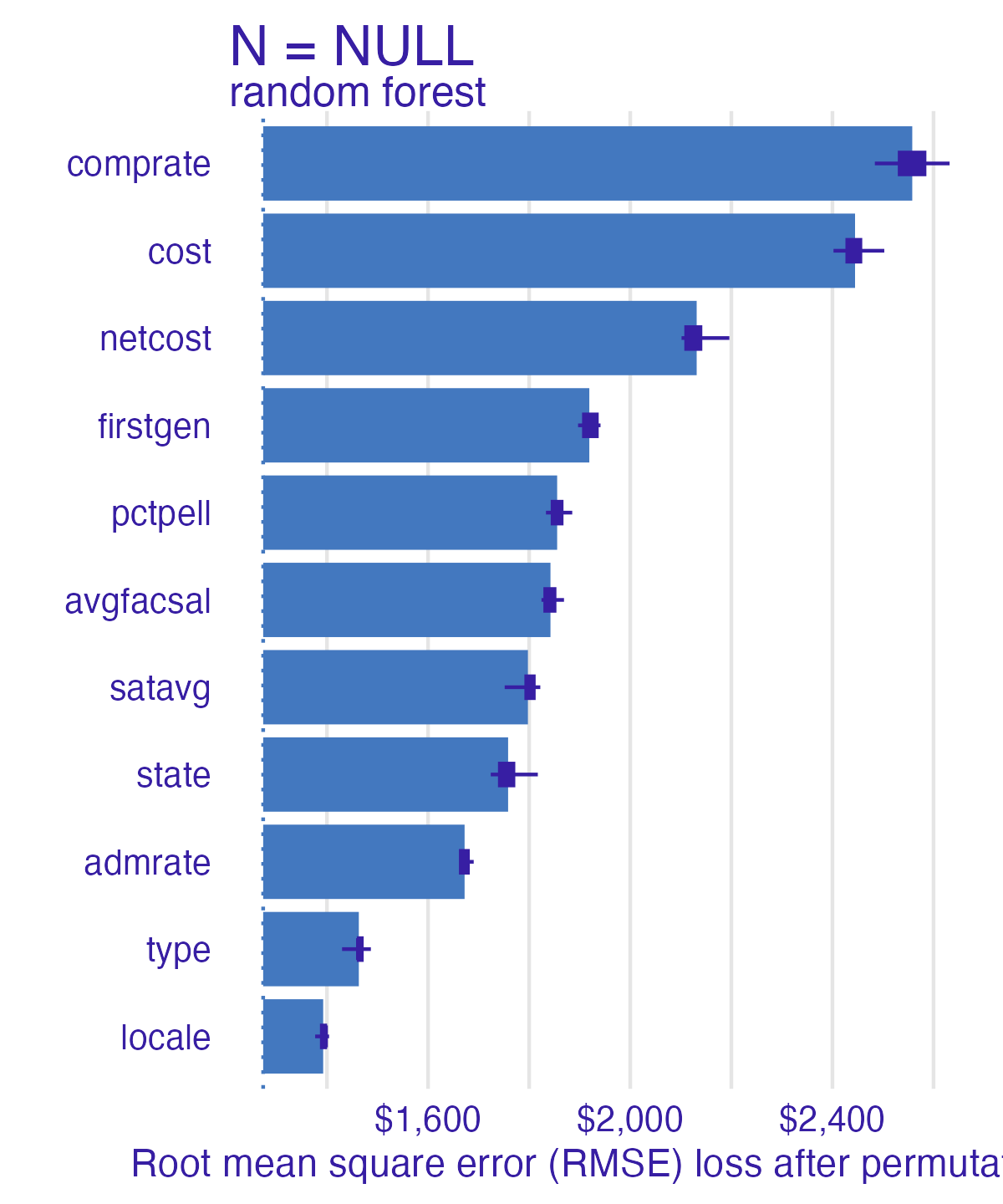
Measuring changes

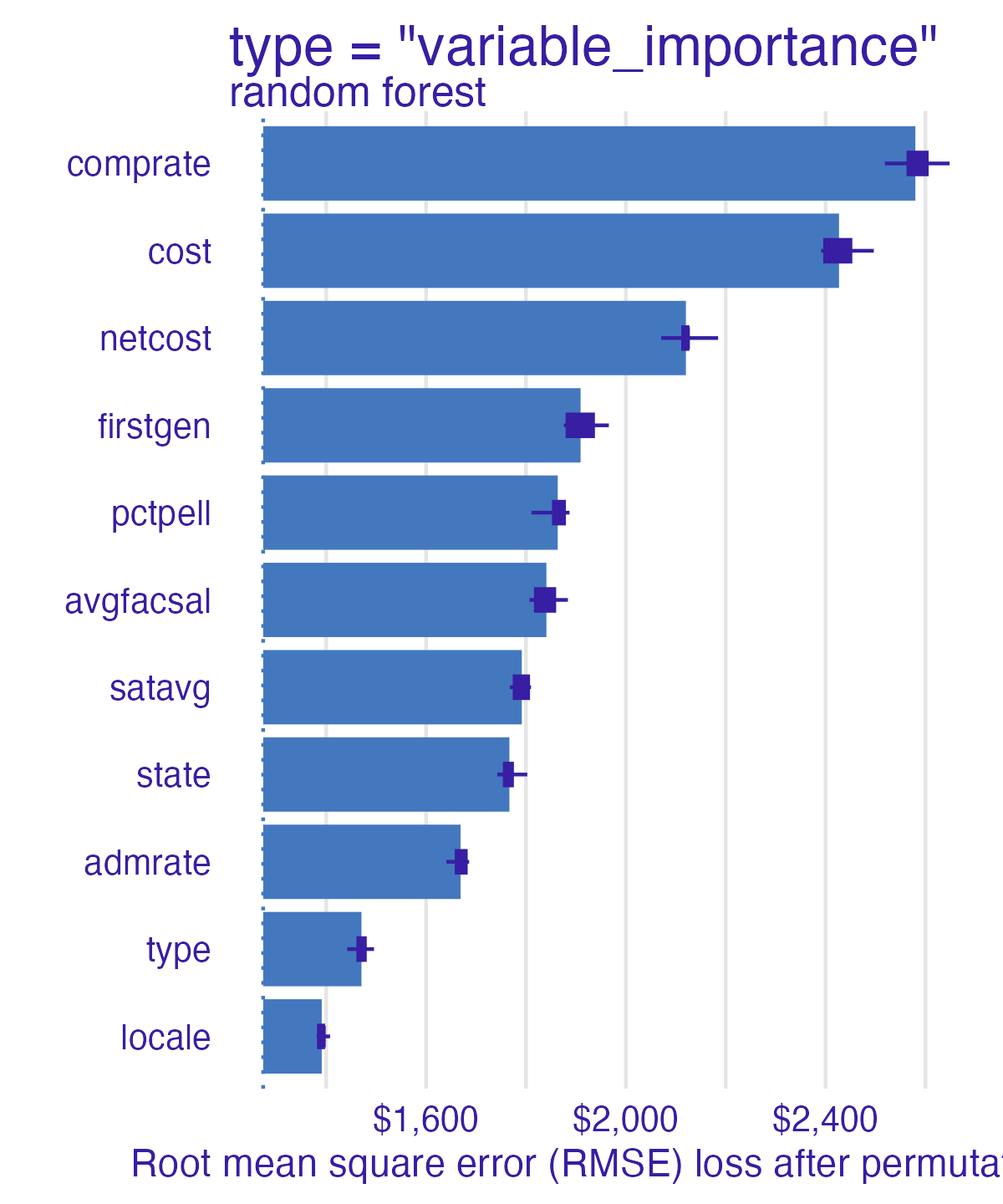
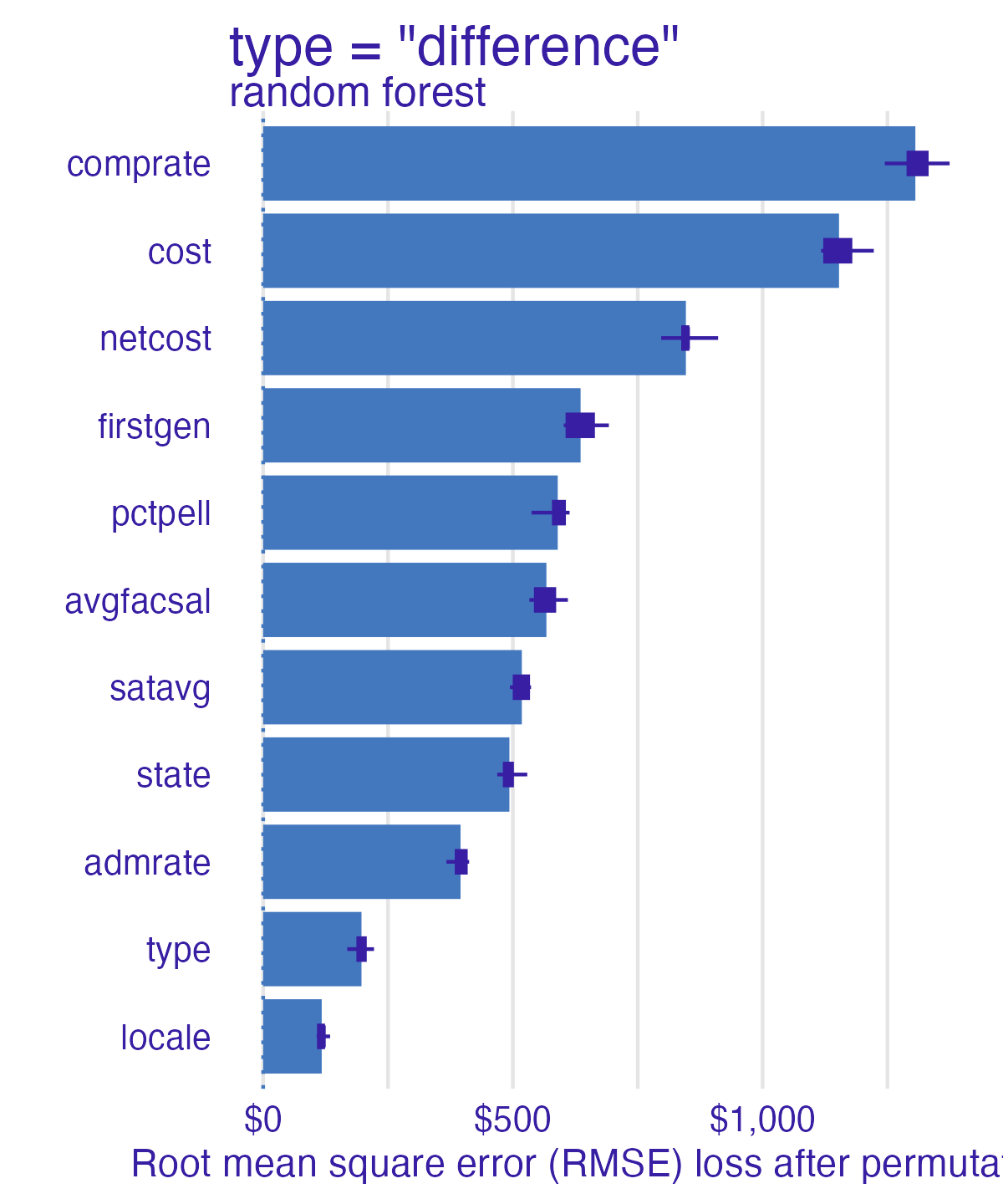
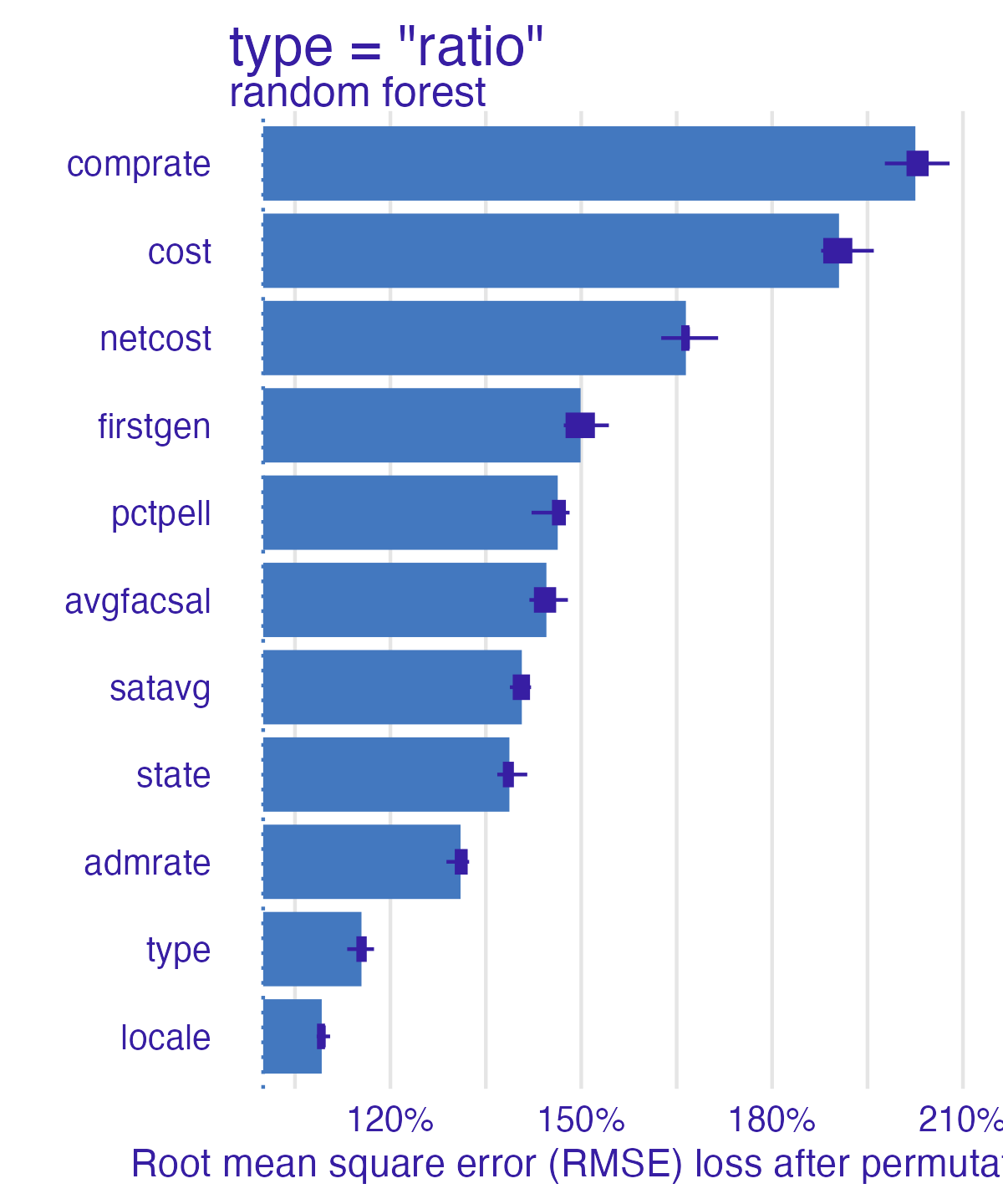
Compare all models

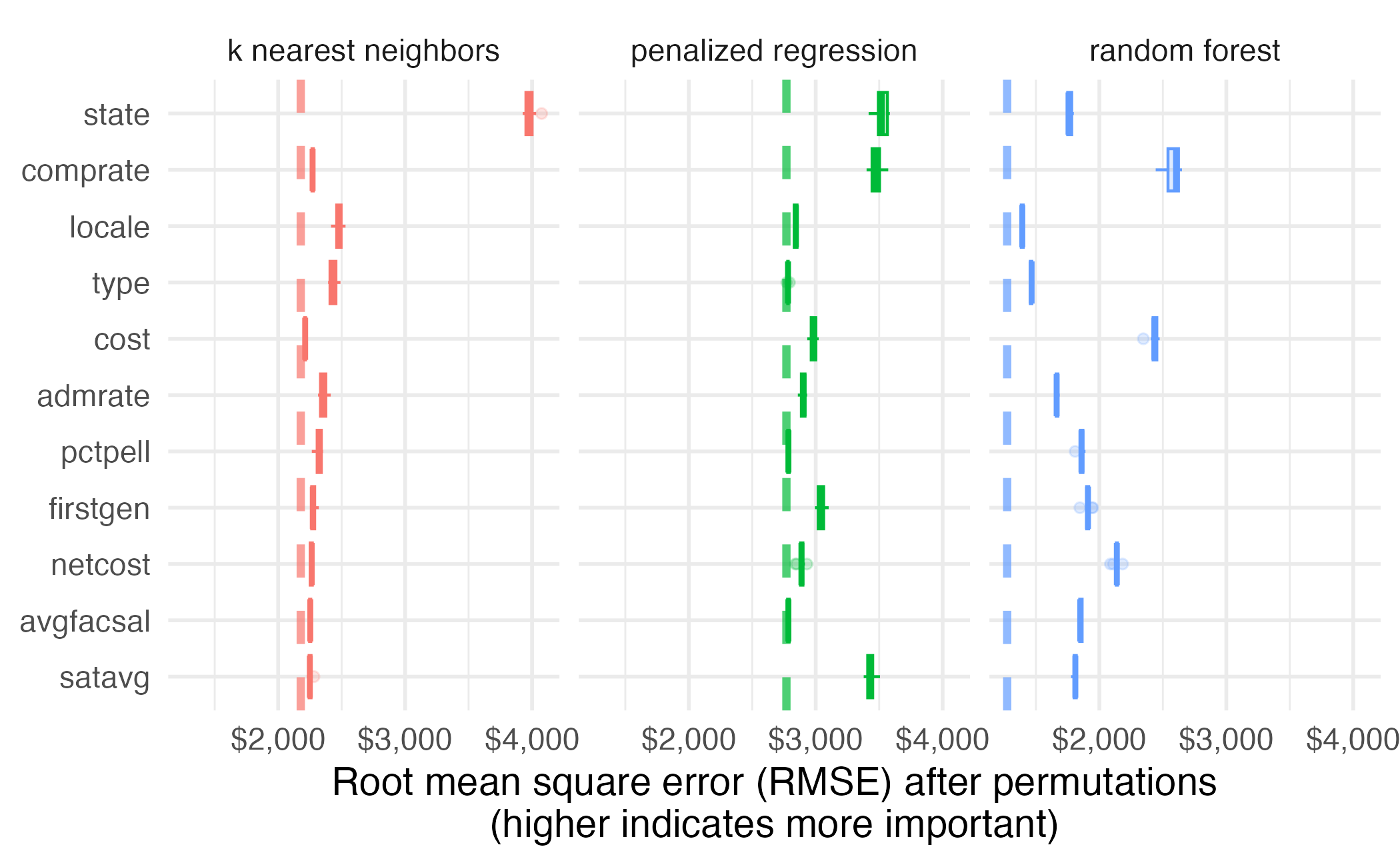
Permutation-based feature importance

Advantages

  • Clear interpretation
  • Succinct measure
  • Does not require retraining the model
  • Takes into account all interactions

Disadvantages

  • Permutation adds randomness to results - results may vary greatly
  • Computationally expensive
  • Linked to the error of the model
  • Need access to the true outcome
  • Takes into account all interactions

Your Turn

  • Review the DALEX code to estimate permutation-based feature importance for the debt prediction models
  • Estimate permutation-based feature importance for the debt prediction models
  • Interpret the resulting statistics - which features are most/least important? How does the model choice influence the results?

Partial dependence plot (PDP)

Individual conditional expectation (ICE)

  • Ceteris peribus - “other things held constant”
  • Marginal effect a feature has on the predictor
  • Counterfactual comparison - what if this observation had \(Y\) value instead of \(X\)?
  • Plot one observation that shows how the observation’s prediction changes when a feature changes
For a selected predictor (x)
1. Construct a grid of j evenly spaced values across the distribution 
   of x: {x1, x2, ..., xj}
2. For i in {1,...,j} do
     | Copy the training data and replace the original values of x 
       with the constant xi
     | Apply given ML model (i.e., obtain vector of predictions)
   End
3. Plot the predictions against x1, x2, ..., xj with lines connecting 
   oberservations that correspond to the same row number in the original 
   training data

Partial dependence plot (PDP)

  • Average multiple ICEs to estimate the marginal effect of a feature on the outcome of interest
For a selected predictor (x)
1. Construct a grid of j evenly spaced values across the distribution
   of x: {x1, x2, ..., xj}
2. For i in {1,...,j} do
     | Copy the training data and replace the original values of x 
       with the constant xi
     | Apply given ML model (i.e., obtain vector of predictions)
     | Average predictions together
   End
3. Plot the averaged predictions against x1, x2, ..., xj

Net cost (PDP)

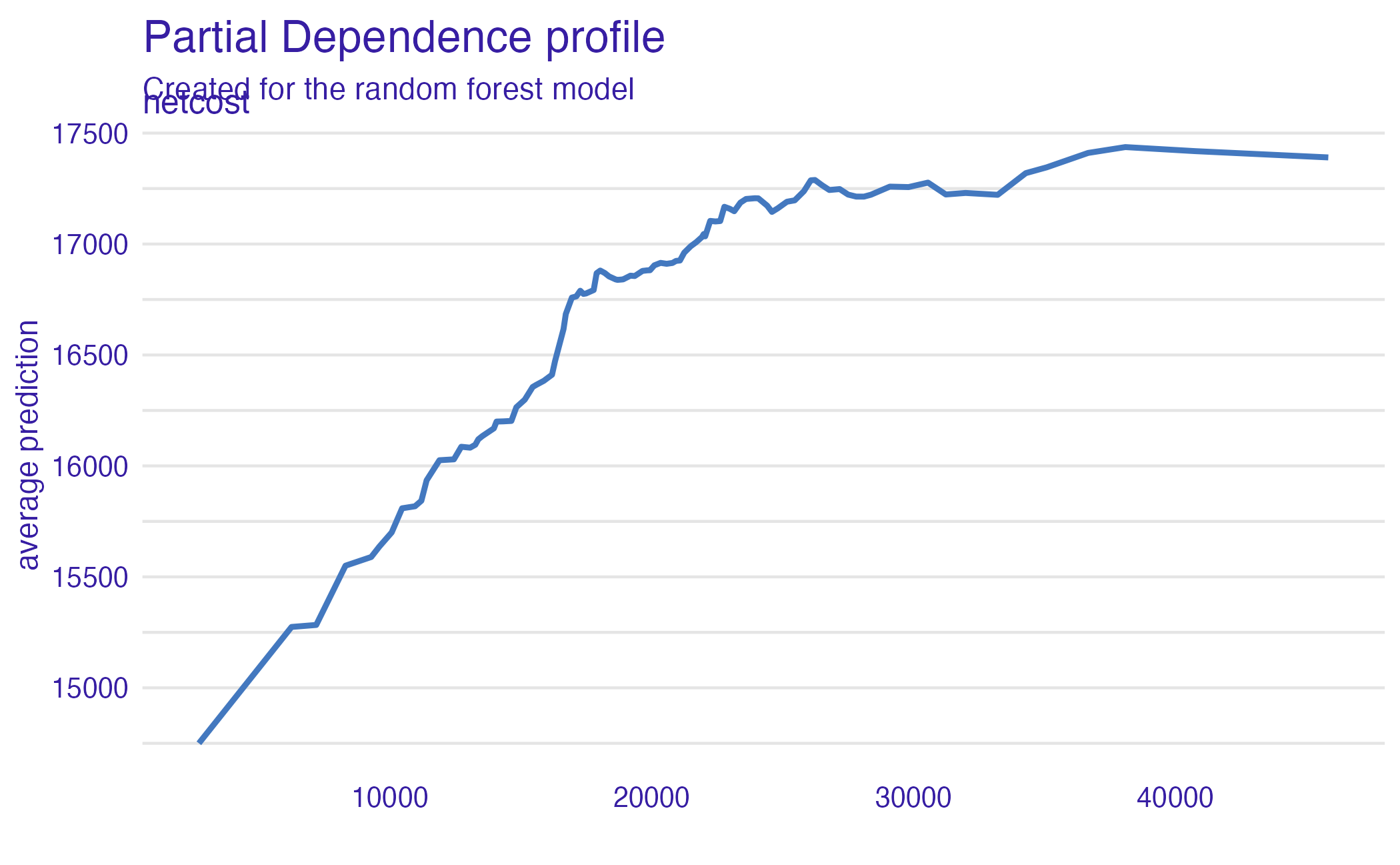
Net cost (PDP + ICE)

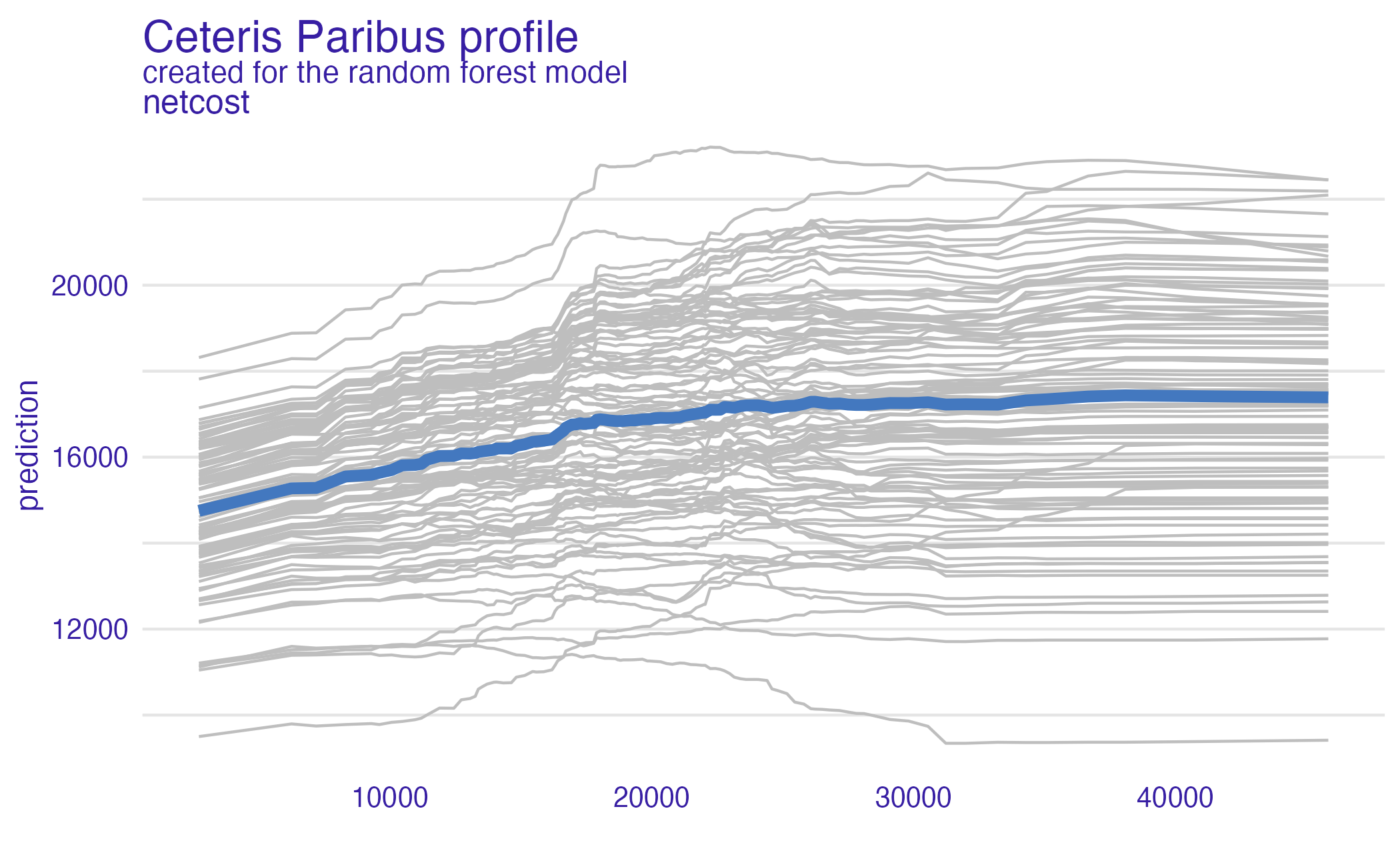
Net cost (PDP + ICE) – all models

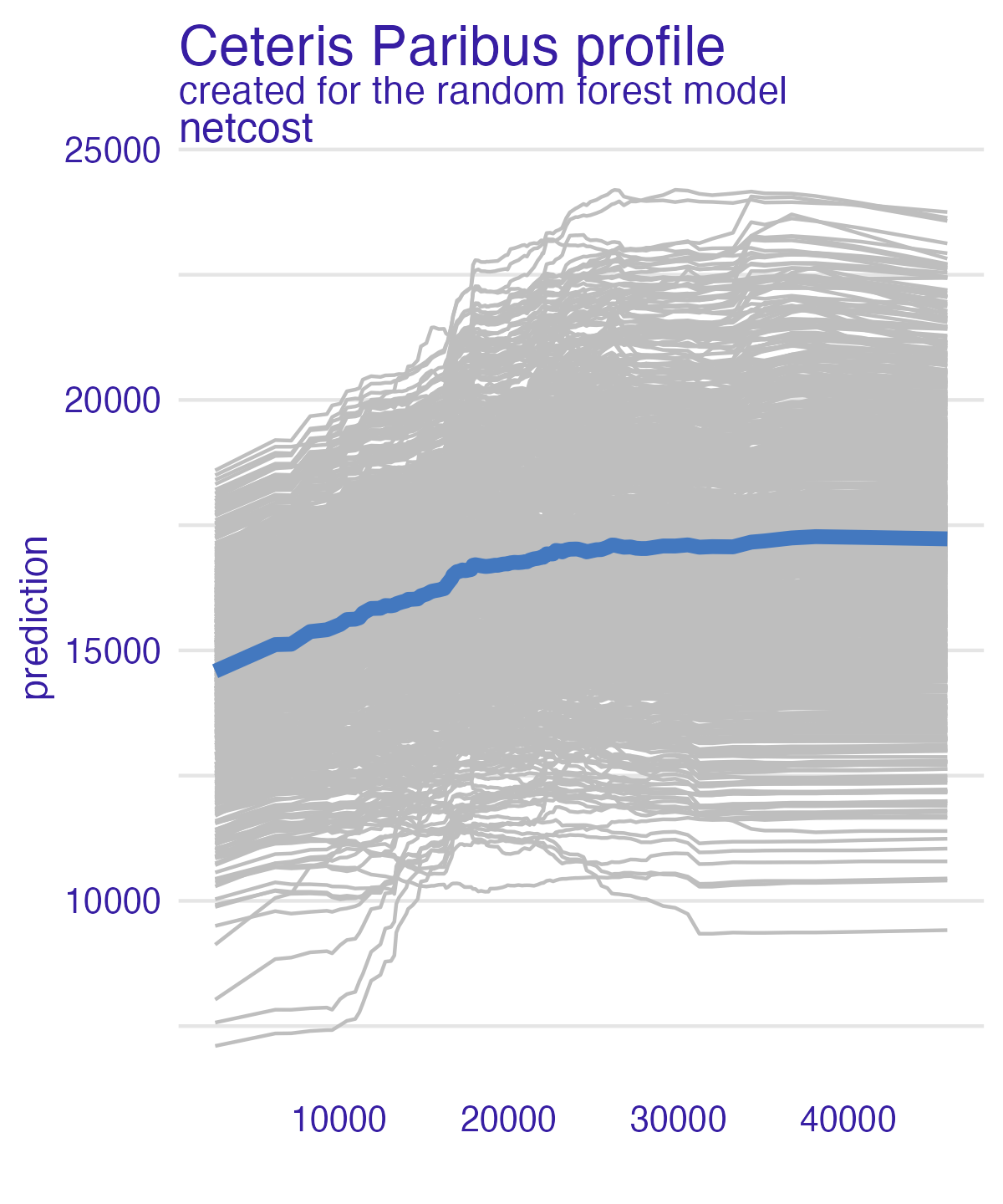
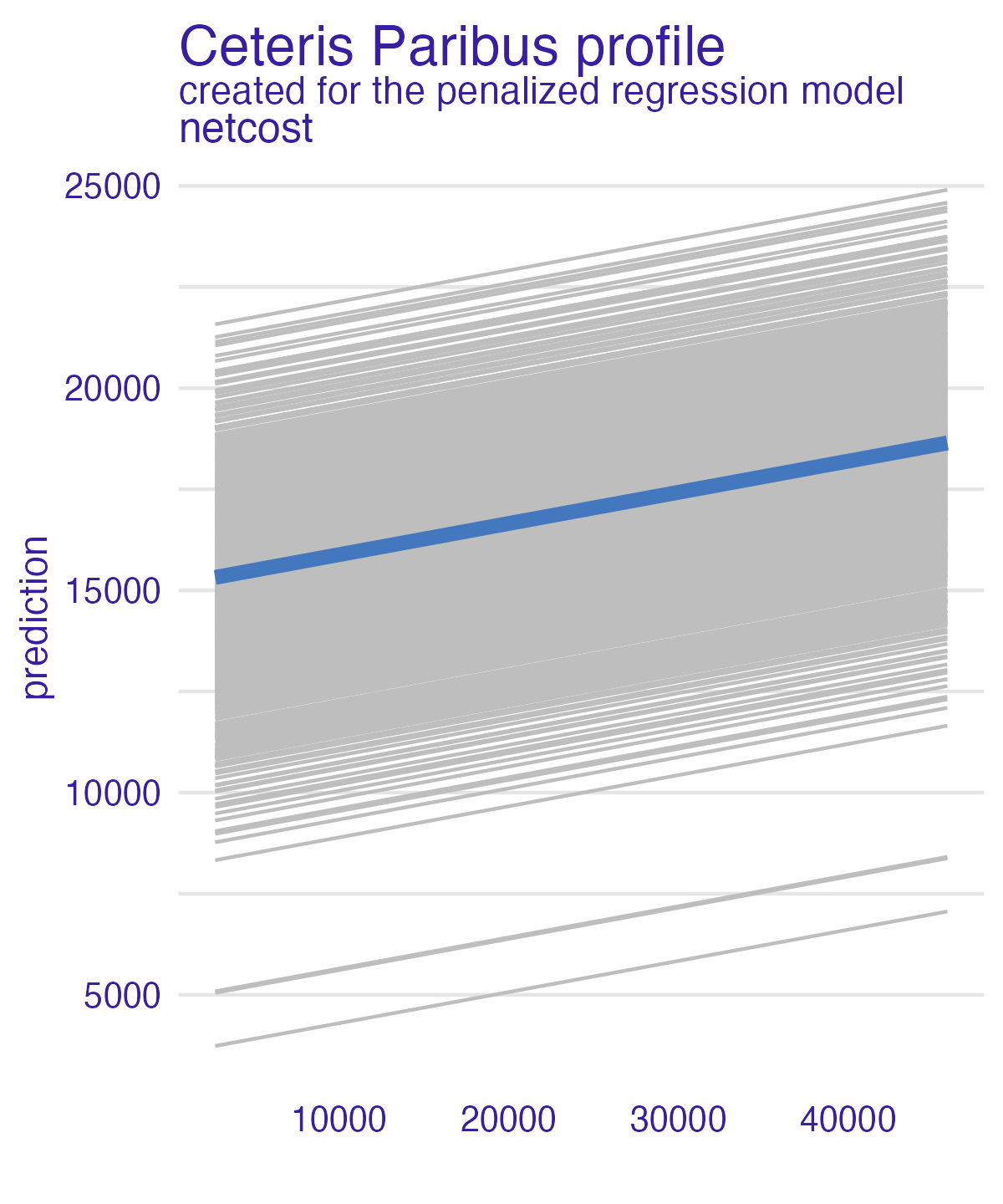
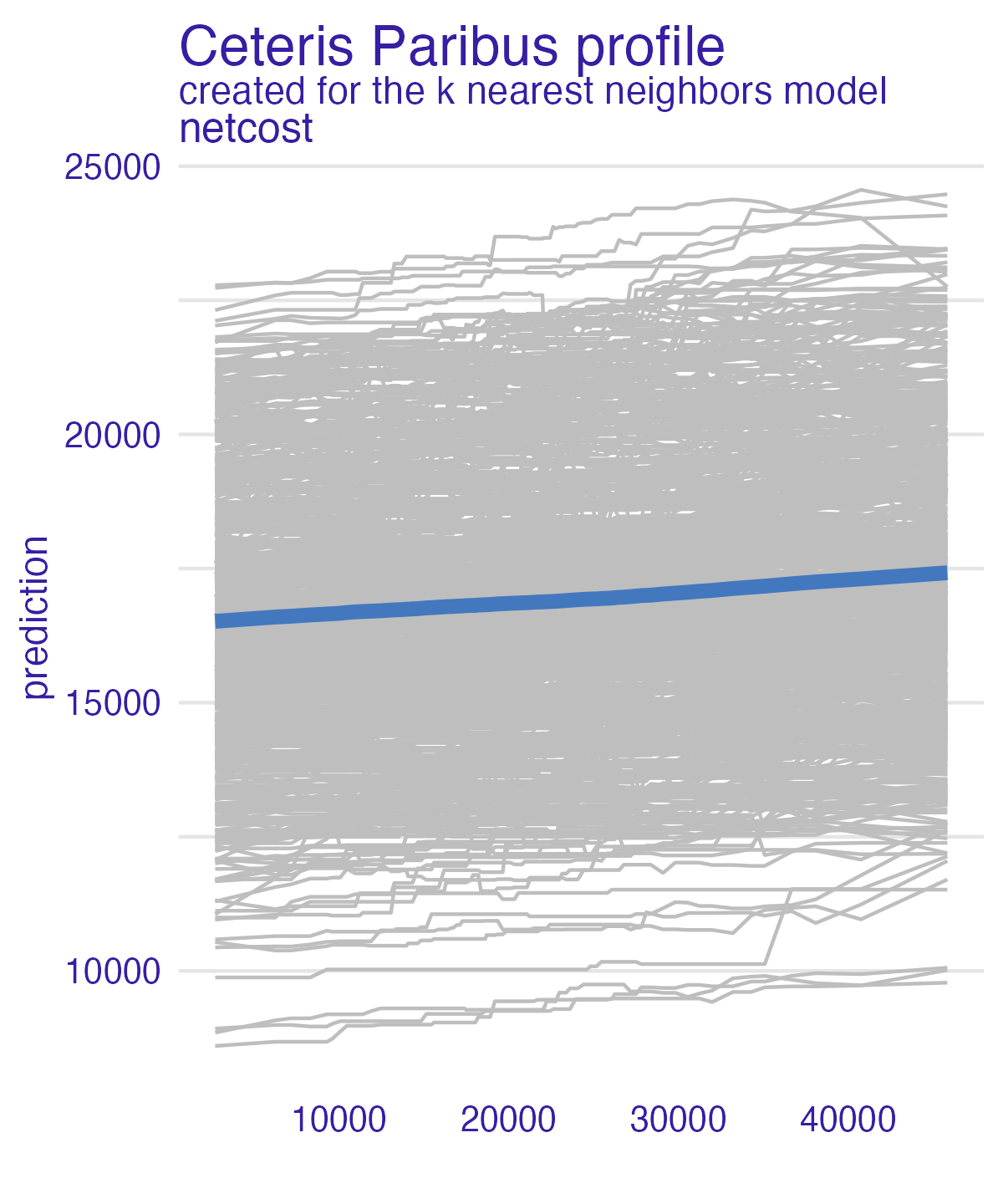
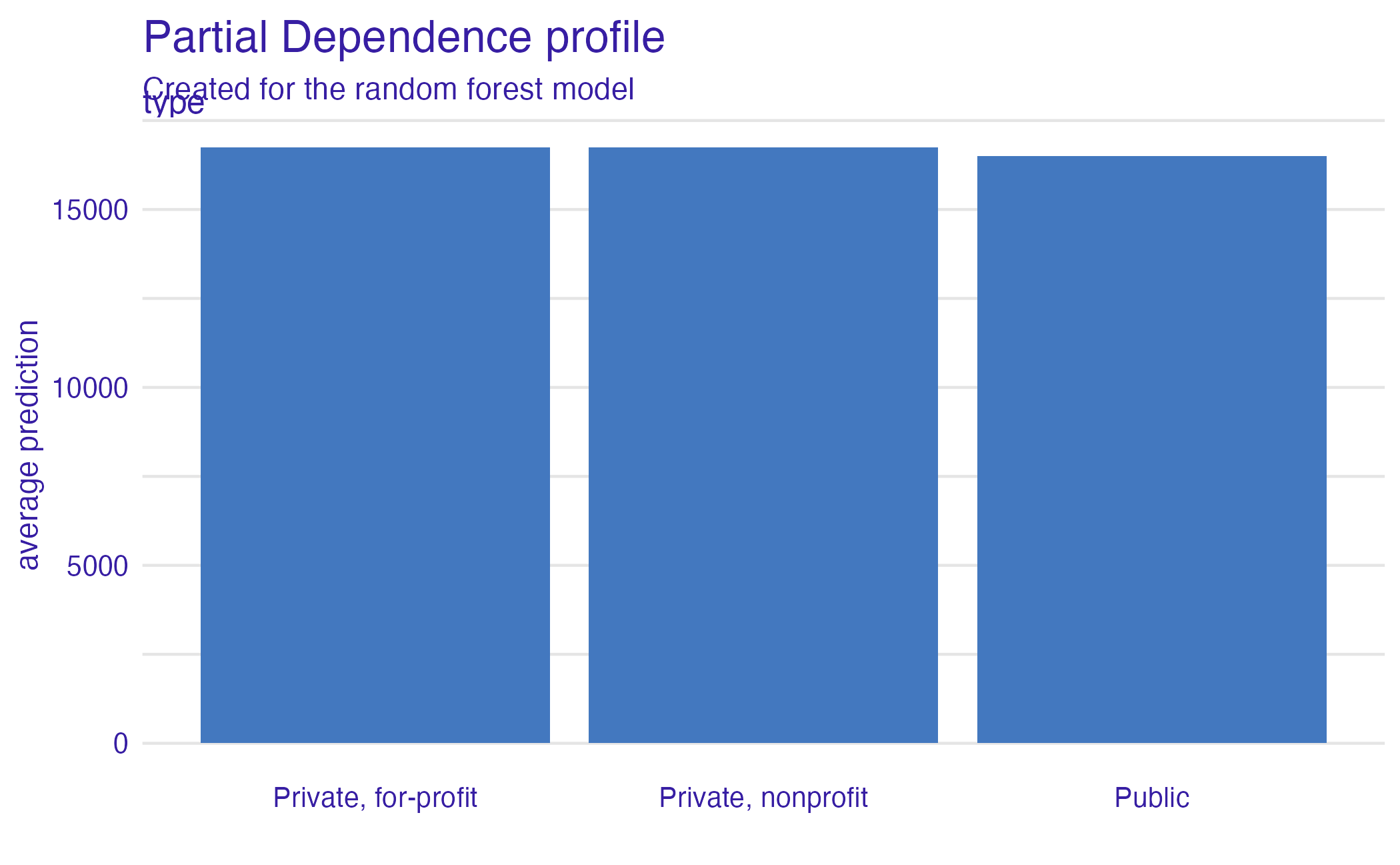
Type (PDP)

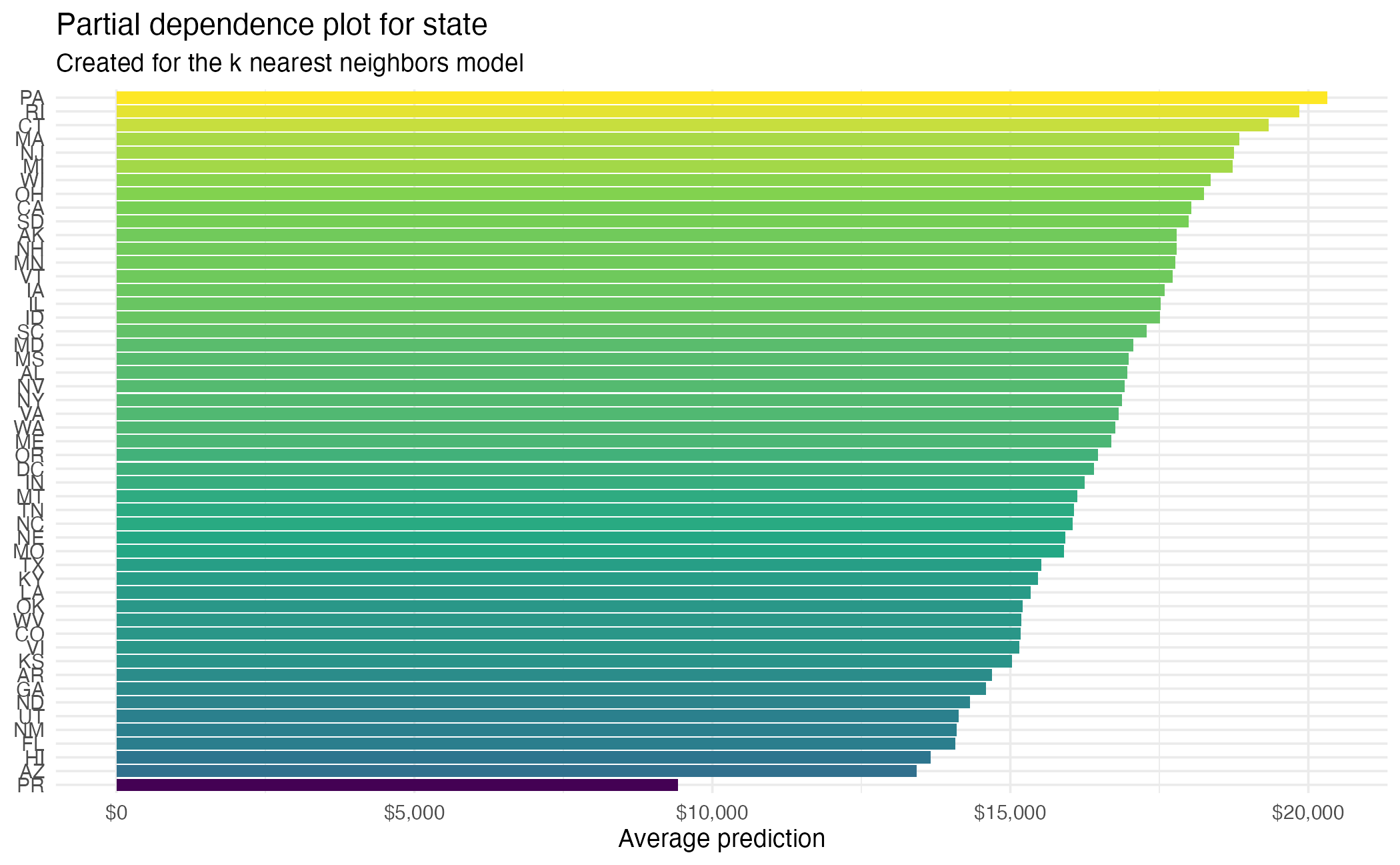
State (PDP)

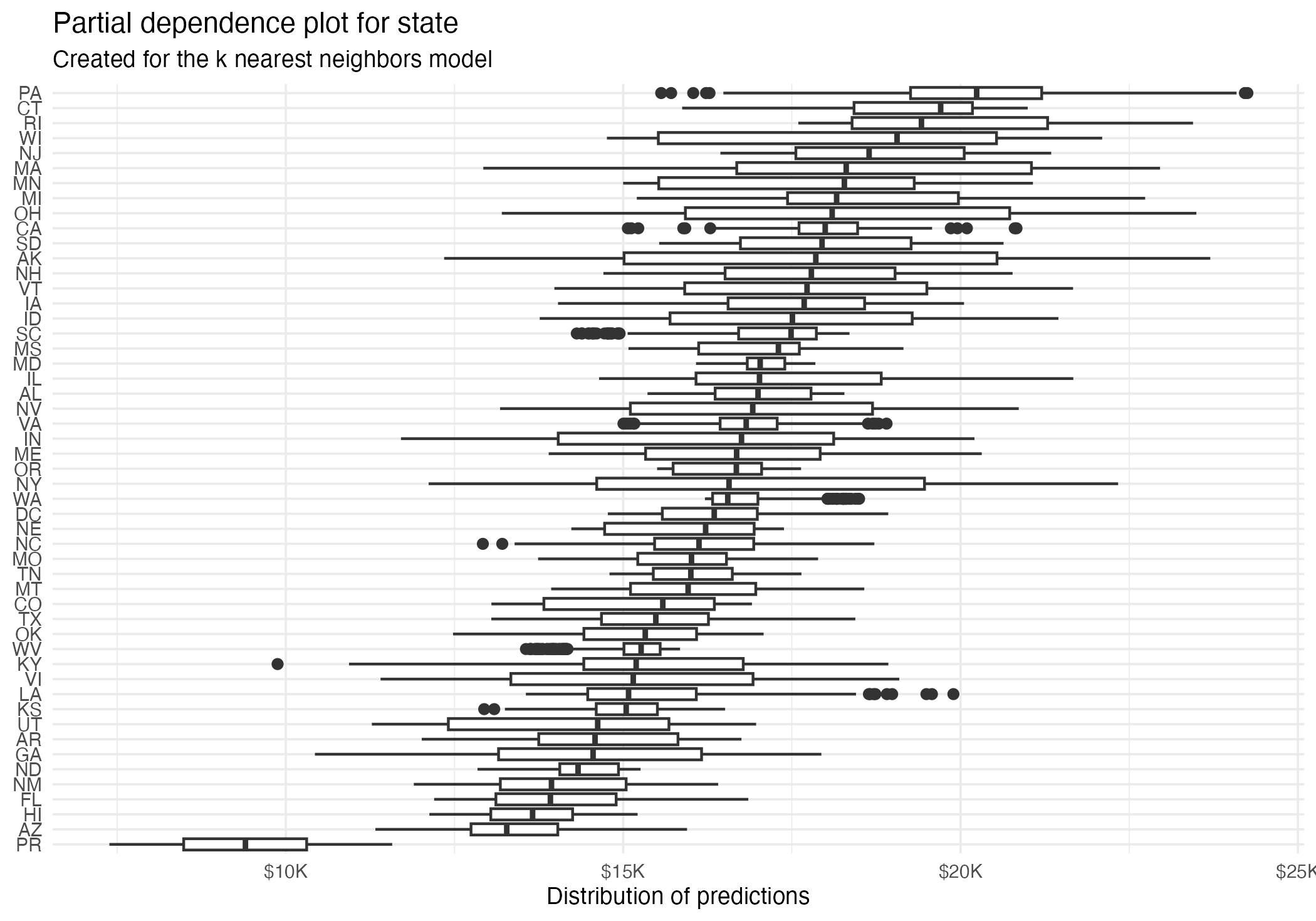
State (PDP + ICE)

Partial dependence plot (PDP)

Advantages

  • Intuitive
  • Clear interpretation (assuming variables are uncorrelated)
  • Straightforward implementation

Disadvantages

  • Limited to one or two variables
  • Assumes independence of features
  • Heterogeneous effects might be hidden - add ICE curves to visualize heterogeneity

Your Turn

  • Review the DALEX code to estimate permutation-based feature importance for the debt prediction models
  • Interpret how the average faculty salary influences the predictions of the debt models

Global surrogate

Global surrogate

  • Use a white-box model to explain the predictions of a black-box model
  • Approximate the global results of a highly complex model with a naturally interpretable model (e.g. simple regression, decision tree)
  • Use a metric such as \(R^2\) to evaluate the performance of the surrogate model

Global surrogate of the penalized regression model

Global surrogate \(R^2 = \text{73%}\)

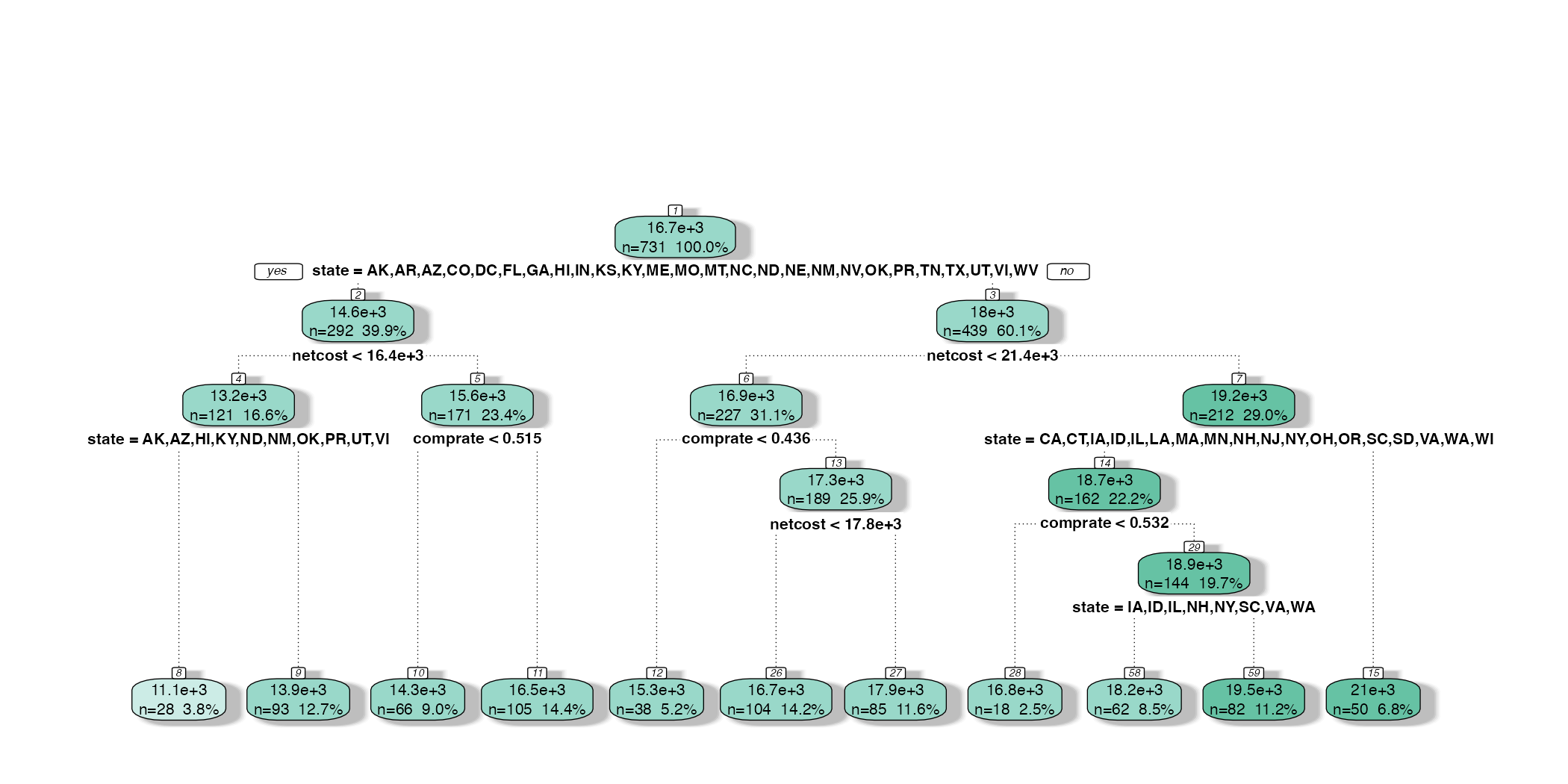
Global surrogate

Advantages

  • Flexible
  • Intuitive
  • Can assess the quality of the surrogate model

Disadvantages

  • Drawing conclusions about the model, not the data
  • How good is good enough for the surrogate?

Your Turn

  • Review the code to fit a global surrogate model
  • Interpret the nearest neighbors model using a decision tree surrogate model

Wrap-up

Wrap-up

  • Interpretability is crucial for understanding and trusting machine learning models
  • Permutation-based feature importance provides insight into the importance of features in a model
  • Partial dependence plots provide a global view of the relationship between a feature and the model’s predictions
  • Global surrogates approximate the predictions of a complex model with a simpler, interpretable model

Additional resources

🔗 info3312.infosci.cornell.edu